Constraints

By -

Constraints

An E-R enterprise schema may define certain constraints to which the contents of a database must conform. In this section, we examine mapping cardinalities and participation constraints, which are two of the most important types of constraints.

Mapping Cardinalities

Mapping cardinalities, or cardinality ratios, express the number of entities to which another entity can be associated via a relationship set.

Mapping cardinalities are most useful in describing binary relationship sets, al- though they can contribute to the description of relationship sets that involve more than two entity sets. In this section, we shall concentrate on only binary relationship sets.

For a binary relationship set R between entity sets A and B, the mapping cardinality must be one of the following:

• One to one. An entity in A is associated with at most one entity in B, and an entity in B is associated with at most one entity in A. (See Figure 2.4a.)

• One to many. An entity in A is associated with any number (zero or more) of entities in B. An entity in B, however, can be associated with at most one entity in A. (See Figure 2.4b.)

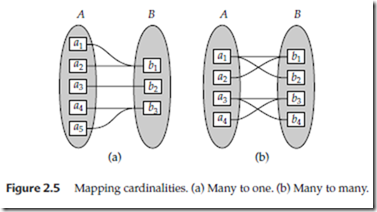
• Many to one. An entity in A is associated with at most one entity in B. An entity in B, however, can be associated with any number (zero or more) of entities in A. (See Figure 2.5a.)

• Many to many. An entity in A is associated with any number (zero or more) of entities in B, and an entity in B is associated with any number (zero or more) of entities in A. (See Figure 2.5b.)

image

The appropriate mapping cardinality for a particular relationship set obviously de- pends on the real-world situation that the relationship set is modeling.

As an illustration, consider the borrower relationship set. If, in a particular bank, a loan can belong to only one customer, and a customer can have several loans, then the relationship set from customer to loan is one to many. If a loan can belong to several customers (as can loans taken jointly by several business partners), the relationship set is many to many. Figure 2.3 depicts this type of relationship.

Participation Constraints

The participation of an entity set E in a relationship set R is said to be total if every entity in E participates in at least one relationship in R. If only some entities in E participate in relationships in R, the participation of entity set E in relationship R is said to be partial. For example, we expect every loan entity to be related to at least one customer through the borrower relationship. Therefore the participation of loan in

image

the relationship set borrower is total. In contrast, an individual can be a bank customer whether or not she has a loan with the bank. Hence, it is possible that only some of the customer entities are related to the loan entity set through the borrower relationship, and the participation of customer in the borrower relationship set is therefore partial.

Comments

Post a Comment

Popular posts from this blog

XML Document Schema

By -
Image
XML Document Schema Databases have schemas, which are used to constrain what information can be stored in the database and to constrain the data types of the stored information. In contrast, by default, XML documents can be created without any associated schema: An el- ement may then have any subelement or attribute. While such freedom may occasionally be acceptable given the self-describing nature of the data format, it is not generally useful when XML documents must be processesed automatically as part of an application, or even when large amounts of related data are to be formatted in XML. Here, we describe the document-oriented schema mechanism included as part of the XML standard, the Document Type Definition , as well as the more recently defined XML S chema . Document Type Definition The document type definition ( D TD ) is an optional part of an XML document. The main purpose of a DTD is much like that of a schema: to constrain and type the information present in the docume
Read more

Extended Relational-Algebra Operations.

By -
Image
Extended Relational-Algebra Operations The basic relational-algebra operations have been extended in several ways. A simple extension is to allow arithmetic operations as part of projection. An important extension is to allow aggregate operations such as computing the sum of the elements of a set, or their average. Another important extension is the outer-join operation, which allows relational-algebra expressions to deal with null values, which model missing information. Generalized Projection The generalized-projectio n operation extends the projection operation by allowing arithmetic functions to be used in the projection list. The generalized projection operation has the form where E is any relational-algebra expression, and each of F 1 , F 2 ,.. . , F n is an arithmetic expression involving constants and attributes in the schema of E . As a special case, the arithmetic expression may be simply an attribute or a constant. For example, suppose we have a relation c r
Read more

Distributed Databases:Concurrency Control in Distributed Databases

By -
Image
Concurrency Control in Distributed Databases We show here how some of the concurrency-control schemes discussed in Chapter 16 can be modified so that they can be used in a distributed environment. We assume that each site participates in the execution of a commit protocol to ensure global trans- action atomicity. The protocols we describe in this section require updates to be done on all replicas of a data item. If any site containing a replica of a data item has failed, updates to the data item cannot be processed. In Section 19.6 we describe protocols that can continue transaction processing even if some sites or links have failed, thereby providing high availability. Locking Protocols The various locking protocols described in Chapter 16 can be used in a distributed environment. The only change that needs to be incorporated is in the way the lock manager deals with replicated data. We present several possible schemes that are applicable to an environment where data can be rep
Read more