Entity-Relationship Diagram

Entity-Relationship Diagram

As we saw briefly in Section 1.4, an E-R diagram can express the overall logical structure of a database graphically. E-R diagrams are simple and clear — qualities that may well account in large part for the widespread use of the E-R model. Such a diagram consists of the following major components:

• Rectangles, which represent entity sets

• Ellipses, which represent attributes

• Diamonds, which represent relationship sets

• Lines, which link attributes to entity sets and entity sets to relationship sets

• Double ellipses, which represent multivalued attributes

• Dashed ellipses, which denote derived attributes

• Double lines, which indicate total participation of an entity in a relation- ship set

• Double rectangles, which represent weak entity sets (described later, in Section 2.6.)

Consider the entity-relationship diagram in Figure 2.8, which consists of two entity sets, customer and loan, related through a binary relationship set borrower. The at- tributes associated with customer are customer-id, customer-name, customer-street, and customer-city. The attributes associated with loan are loan-number and amount. In Figure 2.8, attributes of an entity set that are members of the primary key are underlined.

The relationship set borrower may be many-to-many, one-to-many, many-to-one, or one-to-one. To distinguish among these types, we draw either a directed line (→) or an undirected line ( — ) between the relationship set and the entity set in question.

• A directed line from the relationship set borrower to the entity set loan specifies that borrower is either a one-to-one or many-to-one relationship set, from customer to loan; borrower cannot be a many-to-many or a one-to-many relationship set from customer to loan.

• An undirected line from the relationship set borrower to the entity set loan specifies that borrower is either a many-to-many or one-to-many relationship set from customer to loan.

Returning to the E-R diagram of Figure 2.8, we see that the relationship set borrower is many-to-many. If the relationship set borrower were one-to-many, from customer to loan, then the line from borrower to customer would be directed, with an arrow pointing to the customer entity set (Figure 2.9a). Similarly, if the relationship set borrower were many-to-one from customer to loan, then the line from borrower to loan would have an arrow pointing to the loan entity set (Figure 2.9b). Finally, if the relation- ship set borrower were one-to-one, then both lines from borrower would have arrows:

one pointing to the loan entity set and one pointing to the customer entity set (Figure 2.9c).

If a relationship set has also some attributes associated with it, then we link these attributes to that relationship set. For example, in Figure 2.10, we have the access- date descriptive attribute attached to the relationship set depositor to specify the most recent date on which a customer accessed that account.

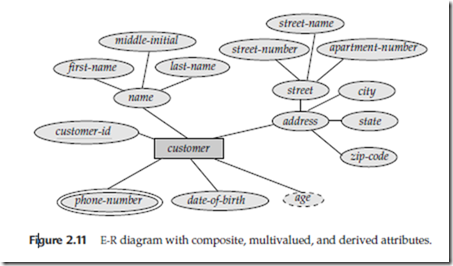
Figure 2.11 shows how composite attributes can be represented in the E-R notation. Here, a composite attribute name, with component attributes first-name, middle-initial, and last-name replaces the simple attribute customer-name of customer. Also, a compos- ite attribute address, whose component attributes are street, city, state, and zip-code re- places the attributes customer-street and customer-city of customer. The attribute street is itself a composite attribute whose component attributes are street-number, street-name, and apartment number.

We indicate roles in E-R diagrams by labeling the lines that connect diamonds to rectangles. Figure 2.12 shows the role indicators manager and worker between the employee entity set and the works-for relationship set.

Nonbinary relationship sets can be specified easily in an E-R diagram. Figure 2.13 consists of the three entity sets employee, job, and branch, related through the relation- ship set works-on.

We can specify some types of many-to-one relationships in the case of nonbinary relationship sets. Suppose an employee can have at most one job in each branch (for example, Jones cannot be a manager and an auditor at the same branch). This constraint can be specified by an arrow pointing to job on the edge from works-on.

We permit at most one arrow out of a relationship set, since an E-R diagram with two or more arrows out of a nonbinary relationship set can be interpreted in two ways. Suppose there is a relationship set R between entity sets A1, A2,... , An, and the only arrows are on the edges to entity sets Ai+1, Ai+2,..., An. Then, the two possible interpretations are:

1. A particular combination of entities from A1, A2,... , Ai can be associated with at most one combination of entities from Ai+1, Ai+2,... , An. Thus, the primary key for the relationship R can be constructed by the union of the primary keys of A1, A2,... , Ai.

2. For each entity set Ak , i < k ≤ n, each combination of the entities from the other entity sets can be associated with at most one entity from Ak . Each set {A1, A2,... , Ak−1, Ak+1,... , An}, for i< k ≤ n, then forms a candidate key.

Each of these interpretations has been used in different books and systems. To avoid confusion, we permit only one arrow out of a relationship set, in which case the two interpretations are equivalent. In Chapter 7 (Section 7.3) we study the notion of functional dependencies, which allow either of these interpretations to be specified in an unambiguous manner.

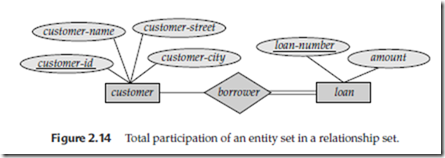
Double lines are used in an E-R diagram to indicate that the participation of an entity set in a relationship set is total; that is, each entity in the entity set occurs in at least one relationship in that relationship set. For instance, consider the relationship borrower between customers and loans. A double line from loan to borrower, as in Figure 2.14, indicates that each loan must have at least one associated customer.

E-R diagrams also provide a way to indicate more complex constraints on the number of times each entity participates in relationships in a relationship set. An edge between an entity set and a binary relationship set can have an associated minimum and maximum cardinality, shown in the form l..h, where l is the minimum and h the maximum cardinality. A minimum value of 1 indicates total participation of the entity set in the relationship set. A maximum value of 1 indicates that the entity participates in at most one relationship, while a maximum value ∗ indicates no limit. Note that a label 1..∗ on an edge is equivalent to a double line.

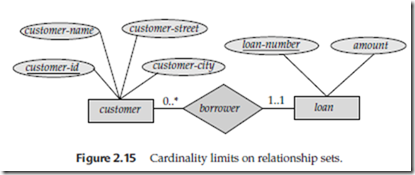
For example, consider Figure 2.15. The edge between loan and borrower has a car- dinality constraint of 1..1, meaning the minimum and the maximum cardinality are both 1. That is, each loan must have exactly one associated customer. The limit 0..∗ on the edge from customer to borrower indicates that a customer can have zero or more loans. Thus, the relationship borrower is one to many from customer to loan, and further the participation of loan in borrower is total.

It is easy to misinterpret the 0..∗ on the edge between customer and borrower, and think that the relationship borrower is many to one from customer to loan — this is exactly the reverse of the correct interpretation.

If both edges from a binary relationship have a maximum value of 1, the relation- ship is one to one. If we had specified a cardinality limit of 1..∗ on the edge between customer and borrower, we would be saying that each customer must have at least one loan.