The Relational Data Model and Relational Database part1.

Relational Model Concepts

The relational Model of Data is based on the concept of a Relation. A Relation is a mathematical concept based on the ideas of sets. The strength of the relational approach to data management comes from the formal foundation provided by the theory of relations. The model was first proposed by Dr. E.F. Codd of IBM in 1970 in the following paper: "A Relational Model for Large Shared Data Banks," Communications of the ACM, June 1970.

Informal Definitions

RELATION:

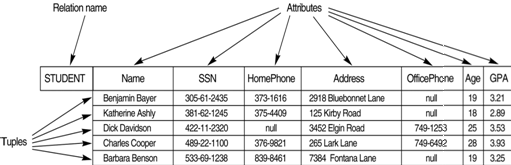
A Relation is table of values. A relation may be thought of as a set of rows. A relation may alternately be though of as a set of columns. Each row represents a fact that corresponds to a real-world entity or relationship. Each row has a value of an item or set of items that uniquely identifies that row in the table. Sometimes row-ids or sequential numbers are assigned to identify the rows in the table. Each column typically is called by its column name or column header or attribute name.

Formal definitions

A Relation may be defined in multiple ways. The Schema of a Relation: R (A1, A2,

.....An) Relation schema R is defined over attributes A1, A2, .....An.

For Example -

CUSTOMER (Cust-id, Cust-name, Address, Phone#)

Here, CUSTOMER is a relation defined over the four attributes Cust-id, Cust-name, Address, Phone#, each of which has a domain or a set of valid values. For example, the domain of Cust-id is 6 digit numbers.

A tuple is an ordered set of values.Each value is derived from an appropriate domain. Each row in the CUSTOMER table may be referred to as a tuple in the table and would consist of four values.

<632895, "John Smith", "101 Main St. Atlanta, GA 30332", "(404) 894-2000">

is a tuple belonging to the CUSTOMER relation.

A relation may be regarded as a set of tuples (rows). Columns in a table are also called attributes of the relation.

A domain has a logical definition: e.g.,

“USA_phone_numbers” are the set of 10 digit phone numbers valid in the U.S.

A domain may have a data-type or a format defined for it. The USA_phone_numbers may have a format: (ddd)-ddd-dddd where each d is a decimal digit. E.g., Dates have various formats such as monthname, date, year or yyyy-mm-dd, or dd mm,yyyy etc.

An attribute designates the role played by the domain. E.g., the domain Date may be used to define attributes “Invoice-date” and “Payment-date”.

The relation is formed over the cartesian product of the sets; each set has values from a domain; that domain is used in a specific role which is conveyed by the attribute name.

For example, attribute Cust-name is defined over the domain of strings of 25 characters. The role these strings play in the CUSTOMER relation is that of the name of customers.

Formally,

r is also called the extension of a relation

Let S1 = {0,1}

Let S2 = {a,b,c}

Let R ⊂ S1 X S2

Then for example: r(R) = {<0,a> , <0,b> , <1,c> } is one possible “state” or “population” or “extension” r of the relation R, defined over domains S1 and S2. It has three tuples.

Example

Characteristics of Relations

Ordering of tuples in a relation r(R): The tuples are not considered to be ordered, even though they appear to be in the tabular form.

Ordering of attributes in a relation schema R (and of values within each tuple): We will consider the attributes in R(A1, A2, ..., An) and the values in t=<v1, v2, ..., vn> to be ordered .

(However, a more general alternative definition of relation does not require this ordering).

Values in a tuple: All values are considered atomic (indivisible). A special null value is used to represent values that are unknown or inapplicable to certain tuples. Notation:

We refer to component values of a tuple t by t[Ai] = vi (the value of attribute Ai for tuple t).

Similarly, t[Au, Av, ..., Aw] refers to the subtuple of t containing the values of attributes Au, Av, ..., Aw, respectively.

Relational Integrity Constraints

Constraints are conditions that must hold on all valid relation instances. There are three main types of constraints:

1. Key constraints

2. Entity integrity constraints

3. Referential integrity constraints

Superkey of R: A set of attributes SK of R such that no two tuples relation instance r(R) will have the same value for SK. That is, fo tuples t1 and t2 in r(R), t1[SK] ≠ t2[SK].

in any valid any distinct

Key of R: A "minimal"

superkey; that is, a superkey K such that removal of any

attribute from K results in a set of attributes that is not a superkey.

Example: The CAR relation schema:

CAR(State, Reg#, SerialNo, Make, Model, Year)

has two keys Key1 = {State, Reg#}, Key2 = {SerialNo}, which are also superkeys.

{SerialNo, Make} is a superkey but not a key.

If a relation has several candidate keys, one is chosen arbitrarily to be the primary key. The primary key attributes are underlined.

Entity Integrity

Relational Database Schema: A set S of relation schemas that belong to the same database. S is the name of the database.

S = {R1, R2, ..., Rn}

Entity Integrity: The primary key attributes PK of each relation schema R in S cannot have null values in any tuple of r(R). This is because primary key values are used to identify the individual tuples.

t[PK] ≠ null for any tuple t in r(R)

Note: Other attributes of R may be similarly constrained to disallow null values, even though they are not members of the primary key.

Referential Integrity

The initial design is typically not complete. Some aspects in the requirements will be represented as relationships.

ER model has three main concepts:

Entities (and their entity types and entity sets) Attributes (simple, composite, multi valued)

Relationships (and their relationship types and relationship sets)

Referential Integrity Constraint

Statement of the constraint

The value in the foreign key column (or columns) FK of the the referencing relation

R1 can be either:

(1) a value of an existing primary key value of the corresponding primary key

PK in the referenced relation R2,, or..

(2) a null.

In case (2), the FK in R1 should not be a part of its own primary key.

Other Types of Constraints

Semantic Integrity Constraints:

It is based on application semantics and cannot be expressed by the model per se

E.g., “the max. no. of hours per employee for all projects he or she works on is 56 hrs per week”

A constraint specification language may have to be used to express these SQL-99 allows triggers and ASSERTIONS to allow for some of these.

Update Operations on Relations

1. INSERT a tuple

2. DELETE a tuple

3. MODIFY a tuple

Update Operations on Relations

Integrity constraints should not be violated by the update operations. Several update operations may have to be grouped together. Updates may propagate to cause other updates automatically. This may be necessary to maintain integrity constraints.

In case of integrity violation, several actions can be taken:

1. Cancel the operation that causes the violation (REJECT option)

2. Perform the operation but inform the user of the violation

3. Trigger additional updates so the violation is corrected (CASCADE option, SET NULL option)

4. Execute a user-specified error-correction routine

The Relational Algebra and Relational Calculus

Introduction

Relational Algebra is a procedural language used for manipulating relations. The relational model gives the structure for relations so that data can be stored in that format but relational algebra enables us to retrieve information from relations. Some advanced SQL queries requires explicit relational algebra operations, most commonly outer join.

Relations are seen as sets of tuples, which means that no duplicates are allowed. SQL behaves differently in some cases. Remember the SQL keyword distinct. SQL is declarative, which means that you tell the DBMS what you want.

Set operations

Relations in relational algebra are seen as sets of tuples, so we can use basic set operations.

Review of concepts and operations from set theory

• Set

• Element

• No duplicate elements

• No order among the elements

• Subset

• Proper subset (with fewer elements)

• Superset

• Union

• Intersection

• Set Difference

• Cartesian product

Relational Algebra

Relational Algebra consists of several groups of operations

Unary Relational Operations SELECT (symbol: s (sigma)) PROJECT (symbol: ∏ (pi))

RENAME (symbol: ρ (rho))

Relational Algebra Operations From Set Theory

UNION ( U ), INTERSECTION ( ∩ ), DIFFERENCE (or MINUS, – ) CARTESIAN PRODUCT ( x )

Binary Relational Operations

JOIN (several variations of JOIN exist) DIVISION

Additional Relational Operations

OUTER JOINS, OUTER UNION

AGGREGATE FUNCTIONS

Unary Relational Operations

SELECT (symbol: s (sigma)) PROJECT (symbol: ∏ (pi))

RENAME (symbol: ρ (rho))

SELECT

The SELECT operation (denoted by σ (sigma)) is used to select a subset of the tuples from a relation based on a selection condition. The selection condition acts as a filter and keeps only those tuples that satisfy the qualifying condition. Tuples satisfying the condition are selected whereas the other tuples are discarded (filtered out)

Database State for COMPANY

• Examples:

– Select the EMPLOYEE tuples whose department number is 4:

DNO = 4 (EMPLOYEE)

– Select the employee tuples whose salary is greater than $30,000:

SALARY > 30,000 (EMPLOYEE)

– In general, the select operation is denoted by σ <selection condition>(R) where the symbol σ (sigma) is used to denote the select operator the selection condition is a Boolean (conditional) expression specified on the attributes of relation R tuples that make the condition true are selected (appear in the result of the operation)

tuples that make the condition false are filtered out (discarded from the result of the operation)

The Boolean expression specified in <selection condition> is made up of a number of clauses of the form:

<attribute name> <comparison op> <constant value> or

<attribute name> <comparison op> <attribute name>

Where <attribute name> is the name of an attribute of R, <comparison op> id normally one of the operations {=,>,>=,<,<=,!=}

Clauses can be arbitrarily connected by the Boolean operators and, or and not

• For example, To select the tuples for all employees who either work in department 4 and make over $25000 per year, or work in department 5 and make over $30000, the select operation should be:

•  (DNO=4 AND Salary>25000 ) OR (DNO=5 AND Salary>30000 ) (EMPLOYEE)

SELECT Operation Properties

– SELECT s is commutative:

 <condition1>(σ < condition2> (R)) = σ <condition2> (σ < condition1> (R))

– A cascade of SELECT operations may be replaced by a single selection with a conjunction of all the conditions:

σ<cond1>(σ< cond2> (σ<cond3>(R)) = σ <cond1> AND < cond2> AND < cond3>(R)