Posts

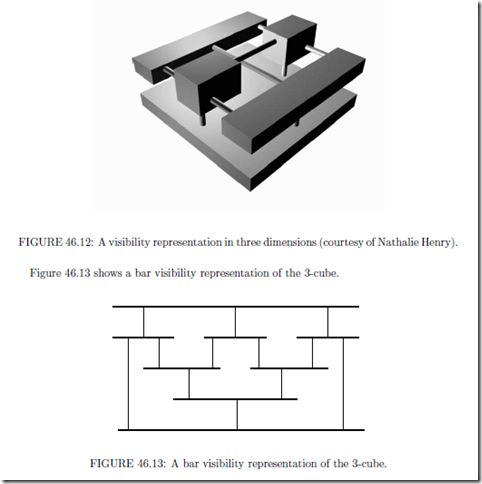
Drawing Graphs:Symmetric Drawing

By -
Image
Symmetric Drawing A graph drawing can have two kinds of symmetry: a x ia l (or reflectional) symmetry and r o t a tional symmetry. For example, see Figure 46.8 . The drawing in Figure 46.8(a) displays four rotational symmetries and Figure 46.8(b) displays one axial symmetry. Figure 46.8(c) displays eight symmetries, four rotational symmetries as well as four axial symmetries. Manning [28] showed that, in general, the problem of determining whether a given graph can be drawn symmetrically is NP-complete. De Fraysseix [9] presents heuristics for symmetric drawings of general graphs. Exact algorithms for finding symmetries in general graphs were presented by Buchheim and Junger [5], and Abelson, Hong and Taylor [1]. There are linear time algorithms available for restricted classes of graphs. Manning and Atallah present a liner time algorithm for detecting symmetries in trees [26], outerplanar graphs [27], and plane graphs [28]. Hong, Eades and Lee present a linear time algorithm
1 comment
Read more

Drawing Graphs:Visibility Drawing

By -
Image
Visibility Drawing In general, a vi sibility representation of a graph has a geometric shape for each vertex, and a “line of sight” for each edge. Different visibility representations involve different kinds of geometric shapes and different restrictions on the “line of sight”. A three dimensional visibility representation of the complete graph on five vertices is in Figure 46.12 . Here the geometric objects are rectangular prisms, and each “line of sight” is parallel to a coordinate axis. Visibility representations have been extensively investigated in both two and three dimensions. For two dimensional graph drawing, the simplest and most common visibility representation uses horizontal line segments (called “bars”) for vertices and vertical line segments for “lines of sight”. More precisely, a b a r visibility representation of a graph G = ( V , E ) consists of a horizontal line segment ω u for each vertex u ∈ V , and a vertical line segment λ e for each edge e ∈ E , such that the
Post a Comment
Read more

Advanced Transaction Processing:Transaction-Processing Monitors

By -
Image
A dvanced Transaction Processing In Chapters 15, 16, and 17, we introduced the concept of a transaction, which is a program unit that accesses—and possibly updates—various data items, and whose execution ensures the preservation of the ACID properties. We discussed in those chapters a variety of schemes for ensuring the ACID properties in an environment where failure can occur, and where the transactions may run concurrently. In this chapter, we go beyond the basic schemes discussed previously, and cover advanced transaction-processing concepts, including transaction-processing monitors, transactional workflows, main-memory databases, real-time databases, long- duration transactions, nested transactions, and multidatabase transactions. Transaction-Processing Monitors T ransaction-processing monitors ( TP monitor s ) are systems that were developed in the 1970s and 1980s, initially in response to a need to support a large number of remote terminals (such as airline-reservation
Post a Comment
Read more

Application Development and Administration:Data Mining

By -
Image
Data Mining The term dat a mining refers loosely to the process of semiautomatically analyzing large databases to find useful patterns. Like knowledge discovery in artificial intelligence (also called machine learning), or statistical analysis, data mining attempts to discover rules and patterns from data. However, data mining differs from machine learning and statistics in that it deals with large volumes of data, stored primarily on disk. That is, data mining deals with “knowledge discovery in databases.” Some types of knowledge discovered from a database can be represented by a set of rules . The following is an example of a rule, stated informally: “Young women with annual incomes greater than $50,000 are the most likely people to buy small sports cars.” Of course such rules are not universally true, and have degrees of “sup- port” and “confidence,” as we shall see. Other types of knowledge are represented by equations relating different variables to each other, or by other mechan
Post a Comment
Read more