Indexing and Hashing:B+-Tree Index Files

B+-Tree Index Files

The main disadvantage of the index-sequential ﬁle organization is that performance degrades as the ﬁle grows, both for index lookups and for sequential scans through the data. Although this degradation can be remedied by reorganization of the ﬁle, frequent reorganizations are undesirable.

The B+-tree index structure is the most widely used of several index structures that maintain their efﬁciency despite insertion and deletion of data. A B+-tree index takes the form of a balanced tree in which every path from the root of the tree to a leaf of the tree is of the same length. Each nonleaf node in the tree has between pn/2l and n children, where n is ﬁxed for a particular tree.

We shall see that the B+-tree structure imposes performance overhead on insertion and deletion, and adds space overhead. The overhead is acceptable even for frequently modiﬁed ﬁles, since the cost of ﬁle reorganization is avoided. Furthermore, since nodes may be as much as half empty (if they have the minimum number of children), there is some wasted space. This space overhead, too, is acceptable given the performance beneﬁts of the B+-tree structure.

Structure of a B+-Tree

A B+-tree index is a multilevel index, but it has a structure that differs from that of the multilevel index-sequential ﬁle. Figure 12.6 shows a typical node of a B+-tree. It contains up to n − 1 search-key values K1, K2,... , Kn − 1, and n pointers P1, P2,... , Pn.

The search-key values within a node are kept in sorted order; thus, if i < j, then Ki < Kj .

We consider ﬁrst the structure of the leaf nodes. For i = 1, 2,... ,n − 1, pointer Pi points to either a ﬁle record with search-key value Ki or to a bucket of pointers, each of which points to a ﬁle record with search-key value Ki. The bucket structure is used only if the search key does not form a primary key, and if the ﬁle is not sorted in the search-key value order. Pointer Pn has a special purpose that we shall discuss shortly.

Figure 12.7 shows one leaf node of a B+-tree for the account ﬁle, in which we have chosen n to be 3, and the search key is branch-name. Note that, since the account ﬁle is ordered by branch-name, the pointers in the leaf node point directly to the ﬁle.

Now that we have seen the structure of a leaf node, let us consider how search-key values are assigned to particular nodes. Each leaf can hold up to n − 1 values. We allow leaf nodes to contain as few as p(n − 1)/2l values. The ranges of values in each leaf do not overlap. Thus, if Li and Lj are leaf nodes and i < j, then every search- key value in Li is less than every search-key value in Lj . If the B+-tree index is to be a dense index, every search-key value must appear in some leaf node.

Now we can explain the use of the pointer Pn. Since there is a linear order on the leaves based on the search-key values that they contain, we use Pn to chain together the leaf nodes in search-key order. This ordering allows for efﬁcient sequential processing of the ﬁle.

The nonleaf nodes of the B+-tree form a multilevel (sparse) index on the leaf nodes.

The structure of nonleaf nodes is the same as that for leaf nodes, except that all pointers are pointers to tree nodes. A nonleaf node may hold up to n pointers, and must

hold at least pn/2l pointers. The number of pointers in a node is called the fanout of the node.

Let us consider a node containing m pointers. For i = 2, 3,... ,m − 1, pointer Pi points to the subtree that contains search-key values less than Ki and greater than or equal to Ki − 1. Pointer Pm points to the part of the subtree that contains those key values greater than or equal to Km − 1, and pointer P1 points to the part of the subtree that contains those search-key values less than K1.

Unlike other nonleaf nodes, the root node can hold fewer than pn/2l pointers; however, it must hold at least two pointers, unless the tree consists of only one node.

It is always possible to construct a B+-tree, for any n, that satisﬁes the preceding requirements. Figure 12.8 shows a complete B+-tree for the account ﬁle (n = 3). For simplicity, we have omitted both the pointers to the ﬁle itself and the null pointers. As an example of a B+-tree for which the root must have less than pn/2l values, Figure 12.9 shows a B+-tree for the account ﬁle with n = 5.

These examples of B+-trees are all balanced. That is, the length of every path from the root to a leaf node is the same. This property is a requirement for a B+-tree. Indeed, the “B” in B+-tree stands for “balanced.” It is the balance property of B+-trees that ensures good performance for lookup, insertion, and deletion.

Queries on B+-Trees

Let us consider how we process queries on a B+-tree. Suppose that we wish to ﬁnd all records with a search-key value of V. Figure 12.10 presents pseudocode for doing so. Intuitively, the procedure works as follows. First, we examine the root node, look- ing for the smallest search-key value greater than V. Suppose that we ﬁnd that this search-key value is Ki. We then follow pointer Pi to another node. If we ﬁnd no such value, then k ≥ Km−1, where m is the number of pointers in the node. In this case we follow Pm to another node. In the node we reached above, again we look for the smallest search-key value greater than V, and once again follow the corresponding pointer as above. Eventually, we reach a leaf node. At the leaf node, if we ﬁnd search key value Ki equals V , then pointer Pi directs us to the desired record or bucket. If the value V is not found in the leaf node, no record with key value V exists.

Thus, in processing a query, we traverse a path in the tree from the root to some leaf node. If there are K search-key values in the ﬁle, the path is no longer than plogIn/2l(K)l.

In practice, only a few nodes need to be accessed, Typically, a node is made to be the same size as a disk block, which is typically 4 kilobytes. With a search-key size of 12 bytes, and a disk-pointer size of 8 bytes, n is around 200. Even with a more conservative estimate of 32 bytes for the search-key size, n is around 100. With n = 100, if we have 1 million search-key values in the ﬁle, a lookup requires only

plog50(1,000,000)l = 4 nodes to be accessed. Thus, at most four blocks need to be read from disk for the lookup. The root node of the tree is usually heavily accessed and is likely to be in the buffer, so typically only three or fewer blocks need to be read from disk.

An important difference between B+-tree structures and in-memory tree struc- tures, such as binary trees, is the size of a node, and as a result, the height of the tree. In a binary tree, each node is small, and has at most two pointers. In a B+-tree, each node is large—typically a disk block—and a node can have a large number of pointers. Thus, B+-trees tend to be fat and short, unlike thin and tall binary trees. In a balanced binary tree, the path for a lookup can be of length plog2(K)l, where K is the number of search-key values. With K = 1,000,000 as in the previous example, a balanced binary tree requires around 20 node accesses. If each node were on a different disk block, 20 block reads would be required to process a lookup, in contrast to the four block reads for the B+-tree.

Updates on B+-Trees

Insertion and deletion are more complicated than lookup, since it may be necessary to split a node that becomes too large as the result of an insertion, or to coalesce nodes (that is, combine nodes) if a node becomes too small (fewer than pn/2l pointers).

Furthermore, when a node is split or a pair of nodes is combined, we must ensure that balance is preserved. To introduce the idea behind insertion and deletion in a B+-tree, we shall assume temporarily that nodes never become too large or too small. Under this assumption, insertion and deletion are performed as deﬁned next.

• Insertion. Using the same technique as for lookup, we ﬁnd the leaf node in which the search-key value would appear. If the search-key value already ap- pears in the leaf node, we add the new record to the ﬁle and, if necessary, add to the bucket a pointer to the record. If the search-key value does not appear, we insert the value in the leaf node, and position it such that the search keys are still in order. We then insert the new record in the ﬁle and, if necessary, create a new bucket with the appropriate pointer.

• Deletion. Using the same technique as for lookup, we ﬁnd the record to be deleted, and remove it from the ﬁle. We remove the search-key value from the leaf node if there is no bucket associated with that search-key value or if the bucket becomes empty as a result of the deletion.

We now consider an example in which a node must be split. Assume that we wish to insert a record with a branch-name value of “Clearview” into the B+-tree of Fig- ure 12.8. Using the algorithm for lookup, we ﬁnd that “Clearview” should appear in the node containing “Brighton” and “Downtown.” There is no room to insert the search-key value “Clearview.” Therefore, the node is split into two nodes. Figure 12.11 shows the two leaf nodes that result from inserting “Clearview” and splitting the node containing “Brighton” and “Downtown.” In general, we take the n search-key

values (the n − 1 values in the leaf node plus the value being inserted), and put the ﬁrst pn/2l in the existing node and the remaining values in a new node.

Having split a leaf node, we must insert the new leaf node into the B+-tree structure. In our example, the new node has “Downtown” as its smallest search-key value.

We need to insert this search-key value into the parent of the leaf node that was split.

The B+-tree of Figure 12.12 shows the result of the insertion. The search-key value “Downtown” was inserted into the parent. It was possible to perform this insertion because there was room for an added search-key value. If there were no room, the parent would have had to be split. In the worst case, all nodes along the path to the root must be split. If the root itself is split, the entire tree becomes deeper.

The general technique for insertion into a B+-tree is to determine the leaf node l into which insertion must occur. If a split results, insert the new node into the parent of node l. If this insertion causes a split, proceed recursively up the tree until either an insertion does not cause a split or a new root is created.

Figure 12.13 outlines the insertion algorithm in pseudocode. In the pseudocode, L.Ki and L.Pi denote the ith value and the ith pointer in node L, respectively. The pseudocode also makes use of the function parent (L) to ﬁnd the parent of a node L.

We can compute a list of nodes in the path from the root to the leaf while initially ﬁnding the leaf node, and can use it later to ﬁnd the parent of any node in the path efﬁciently. The pseudocode refers to inserting an entry (V, P ) into a node. In the case of leaf nodes, the pointer to an entry actually precedes the key value, so the leaf node actually stores P before V . For internal nodes, P is stored just after V .

We now consider deletions that cause tree nodes to contain too few pointers. First, let us delete “Downtown” from the B+-tree of Figure 12.12. We locate the entry for “Downtown” by using our lookup algorithm. When we delete the entry for “Downtown” from its leaf node, the leaf becomes empty. Since, in our example, n = 3 and 0 < p(n − 1)/2l, this node must be eliminated from the B+-tree. To delete a leaf node,

we must delete the pointer to it from its parent. In our example, this deletion leaves the parent node, which formerly contained three pointers, with only two pointers.

Since 2 ≥ pn/2l, the node is still sufﬁciently large, and the deletion operation is complete. The resulting B+-tree appears in Figure 12.14.

When we make a deletion from a parent of a leaf node, the parent node itself may become too small. That is exactly what happens if we delete “Perryridge” from the B+-tree of Figure 12.14. Deletion of the Perryridge entry causes a leaf node to become empty. When we delete the pointer to this node in the latter’s parent, the parent is left with only one pointer. Since n = 3, pn/2l = 2, and thus only one pointer is too few.

However, since the parent node contains useful information, we cannot simply delete it. Instead, we look at the sibling node (the nonleaf node containing the one search key, Mianus). This sibling node has room to accommodate the information contained in our now-too-small node, so we coalesce these nodes, such that the sibling node now contains the keys “Mianus” and “Redwood.” The other node (the node contain- ing only the search key “Redwood”) now contains redundant information and can be deleted from its parent (which happens to be the root in our example). Figure 12.15 shows the result. Notice that the root has only one child pointer after the deletion, so it is deleted and its sole child becomes the root. So the depth of the B+-tree has been decreased by 1.

It is not always possible to coalesce nodes. As an illustration, delete “Perryridge” from the B+-tree of Figure 12.12. In this example, the “Downtown” entry is still part of the tree. Once again, the leaf node containing “Perryridge” becomes empty. The parent of the leaf node becomes too small (only one pointer). However, in this example, the sibling node already contains the maximum number of pointers: three.

Thus, it cannot accommodate an additional pointer. The solution in this case is to redistribute the pointers such that each sibling has two pointers. The result appears in

Figure 12.16. Note that the redistribution of values necessitates a change of a search- key value in the parent of the two siblings.

In general, to delete a value in a B+-tree, we perform a lookup on the value and delete it. If the node is too small, we delete it from its parent. This deletion results in recursive application of the deletion algorithm until the root is reached, a parent remains adequately full after deletion, or redistribution is applied.

Figure 12.17 outlines the pseudocode for deletion from a B+-tree. The procedure swap variables(L, LI) merely swaps the values of the (pointer) variables L and LI; this swap has no effect on the tree itself. The pseudocode uses the condition “too few pointers/values.” For nonleaf nodes, this criterion means less than pn/2l pointers; for leaf nodes, it means less than p(n − 1)/2l values. The pseudocode redistributes entries by borrowing a single entry from an adjacent node. We can also redistribute entries by repartitioning entries equally between the two nodes. The pseudocode refers to deleting an entry (V, P ) from a node. In the case of leaf nodes, the pointer to an entry actually precedes the key value, so the pointer P precedes the key value V . For internal nodes, P follows the key value V .

It is worth noting that, as a result of deletion, a key value that is present in an internal node of the B+-tree may not be present at any leaf of the tree.

Although insertion and deletion operations on B+-trees are complicated, they require relatively few I/O operations, which is an important beneﬁt since I/O operations are expensive. It can be shown that the number of I/O operations needed for a worst-case insertion or deletion is proportional to log (K), where n is the maximum number of pointers in a node, and K is the number of search-key values. In other words, the cost of insertion and deletion operations is proportional to the height of the B+-tree, and is therefore low. It is the speed of operation on B+-trees that makes them a frequently used index structure in database implementations.

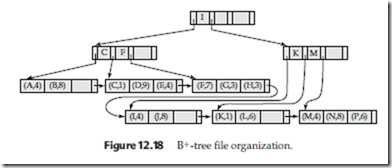
B+-Tree File Organization

As mentioned in Section 12.3, the main drawback of index-sequential ﬁle organization is the degradation of performance as the ﬁle grows: With growth, an increasing percentage of index records and actual records become out of order, and are stored in overﬂow blocks. We solve the degradation of index lookups by using B+-tree indices on the ﬁle. We solve the degradation problem for storing the actual records by using the leaf level of the B+-tree to organize the blocks containing the actual records. We

use the B+-tree structure not only as an index, but also as an organizer for records in a ﬁle. Ina B+-tree ﬁle organization, the leaf nodes of the tree store records, instead of storing pointers to records. Figure 12.18 shows an example of a B+-tree ﬁle organiza- tion. Since records are usually larger than pointers, the maximum number of records that can be stored in a leaf node is less than the number of pointers in a nonleaf node. However, the leaf nodes are still required to be at least half full.

Insertion and deletion of records from a B+-tree ﬁle organization are handled in the same way as insertion and deletion of entries in a B+-tree index. When a record with a given key value v is inserted, the system locates the block that should contain the record by searching the B+-tree for the largest key in the tree that is ≤ v. If the block located has enough free space for the record, the system stores the record in the block. Otherwise, as in B+-tree insertion, the system splits the block in two, and redistributes the records in it (in the B+-tree–key order) to create space for the new record.

The split propagates up the B+-tree in the normal fashion. When we delete a record, the system ﬁrst removes it from the block containing it. If a block B becomes less than half full as a result, the records in B are redistributed with the records in an adjacent block BI. Assuming ﬁxed-sized records, each block will hold at least one-half as many records as the maximum that it can hold. The system updates the nonleaf nodes of the B+-tree in the usual fashion.

When we use a B+-tree for ﬁle organization, space utilization is particularly important, since the space occupied by the records is likely to be much more than the space occupied by keys and pointers. We can improve the utilization of space in a B+- tree by involving more sibling nodes in redistribution during splits and merges. The technique is applicable to both leaf nodes and internal nodes, and works as follows.

During insertion, if a node is full the system attempts to redistribute some of its entries to one of the adjacent nodes, to make space for a new entry. If this attempt fails because the adjacent nodes are themselves full, the system splits the node, and splits the entries evenly among one of the adjacent nodes and the two nodes that it obtained by splitting the original node. Since the three nodes together contain one more record than can ﬁt in two nodes, each node will be about two-thirds full. More precisely, each node will have at least l2n/3J entries, where n is the maximum number of entries that the node can hold. (lxJ denotes the greatest integer that is less than or equal to x; that is, we drop the fractional part, if any.)

During deletion of a record, if the occupancy of a node falls below l2n/3J, the system attempts to borrow an entry from one of the sibling nodes. If both sibling nodes have l2n/3J records, instead of borrowing an entry, the system redistributes the entries in the node and in the two siblings evenly between two of the nodes, and deletes the third node. We can use this approach because the total number of entries is 3l2n/3J−1, which is less than 2n. With three adjacent nodes used for redistribution, each node can be guaranteed to have l3n/4J entries. In general, if m nodes (m − 1

siblings) are involved in redistribution, each node can be guaranteed to contain at least l(m − 1)n/mJ entries. However, the cost of update becomes higher as more sibling nodes are involved in the redistribution.

B-Tree Index Files

B-tree indices are similar to B+-tree indices. The primary distinction between the two approaches is that a B-tree eliminates the redundant storage of search-key values. In the B+-tree of Figure 12.12, the search keys “Downtown,” “Mianus,” “Redwood,” and “Perryridge” appear twice. Every search-key value appears in some leaf node; several are repeated in nonleaf nodes.

A B-tree allows search-key values to appear only once. Figure 12.19 shows a B-tree that represents the same search keys as the B+-tree of Figure 12.12. Since search keys are not repeated in the B-tree, we may be able to store the index in fewer tree nodes than in the corresponding B+-tree index. However, since search keys that appear in nonleaf nodes appear nowhere else in the B-tree, we are forced to include an additional pointer ﬁeld for each search key in a nonleaf node. These additional pointers point to either ﬁle records or buckets for the associated search key.

A generalized B-tree leaf node appears in Figure 12.20a; a nonleaf node appears in Figure 12.20b. Leaf nodes are the same as in B+-trees. In nonleaf nodes, the pointers Pi are the tree pointers that we used also for B+-trees, while the pointers Bi are bucket or ﬁle-record pointers. In the generalized B-tree in the ﬁgure, there are n − 1 keys in the leaf node, but there are m − 1 keys in the nonleaf node. This discrepancy occurs because nonleaf nodes must include pointers Bi, thus reducing the number of

search keys that can be held in these nodes. Clearly, m< n, but the exact relationship between m and n depends on the relative size of search keys and pointers.

The number of nodes accessed in a lookup in a B-tree depends on where the search key is located. A lookup on a B+-tree requires traversal of a path from the root of the tree to some leaf node. In contrast, it is sometimes possible to ﬁnd the desired value in a B-tree before reaching a leaf node. However, roughly n times as many keys are stored in the leaf level of a B-tree as in the nonleaf levels, and, since n is typically large, the beneﬁt of ﬁnding certain values early is relatively small. Moreover, the fact that fewer search keys appear in a nonleaf B-tree node, compared to B+-trees, implies that a B-tree has a smaller fanout and therefore may have depth greater than that of the corresponding B+-tree. Thus, lookup in a B-tree is faster for some search keys but slower for others, although, in general, lookup time is still proportional to the logarithm of the number of search keys.

Deletion in a B-tree is more complicated. In a B+-tree, the deleted entry always appears in a leaf. In a B-tree, the deleted entry may appear in a nonleaf node. The proper value must be selected as a replacement from the subtree of the node containing the deleted entry. Speciﬁcally, if search key Ki is deleted, the smallest search key appearing in the subtree of pointer Pi +1 must be moved to the ﬁeld formerly occupied by Ki. Further actions need to be taken if the leaf node now has too few entries. In contrast, insertion in a B-tree is only slightly more complicated than is insertion in a B+-tree.

The space advantages of B-trees are marginal for large indices, and usually do not outweigh the disadvantages that we have noted. Thus, many database system implementers prefer the structural simplicity of a B+-tree. The exercises explore details of the insertion and deletion algorithms for B-trees.

Search This Blog

Database Management System course