Concurrency Control:Multiple Granularity

Multiple Granularity

In the concurrency-control schemes described thus far, we have used each individual data item as the unit on which synchronization is performed.

There are circumstances, however, where it would be advantageous to group several data items, and to treat them as one individual synchronization unit. For example, if a transaction Ti needs to access the entire database, and a locking protocol is used, then Ti must lock each item in the database. Clearly, executing these locks is time consuming. It would be better if Ti could issue a single lock request to lock the

entire database. On the other hand, if transaction Tj needs to access only a few data items, it should not be required to lock the entire database, since otherwise concurrency is lost.

What is needed is a mechanism to allow the system to define multiple levels of granularity. We can make one by allowing data items to be of various sizes and defining a hierarchy of data granularities, where the small granularities are nested within larger ones. Such a hierarchy can be represented graphically as a tree. Note that the tree that we describe here is significantly different from that used by the tree protocol (Section 16.1.5). A nonleaf node of the multiple-granularity tree represents the data associated with its descendants. In the tree protocol, each node is an independent data item.

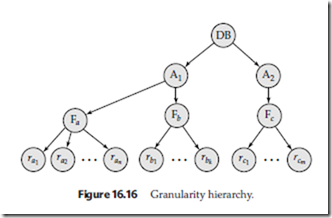
As an illustration, consider the tree of Figure 16.16, which consists of four levels of nodes. The highest level represents the entire database. Below it are nodes of type area; the database consists of exactly these areas. Each area in turn has nodes of type file as its children. Each area contains exactly those files that are its child nodes. No file is in more than one area. Finally, each file has nodes of type record. As before, the file consists of exactly those records that are its child nodes, and no record can be present in more than one file.

Each node in the tree can be locked individually. As we did in the two-phase locking protocol, we shall use shared and exclusive lock modes. When a transaction locks a node, in either shared or exclusive mode, the transaction also has implicitly locked all the descendants of that node in the same lock mode. For example, if transaction Ti gets an explicit lock on file Fc of Figure 16.16, in exclusive mode, then it has an implicit lock in exclusive mode all the records belonging to that file. It does not need to lock the individual records of Fc explicitly.

Suppose that transaction Tj wishes to lock record rb6 of file Fb. Since Ti has locked Fb explicitly, it follows that rb6 is also locked (implicitly). But, when Tj issues a lock request for rb6 , rb6 is not explicitly locked! How does the system determine whether Tj can lock rb6 ? Tj must traverse the tree from the root to record rb6 . If any node in that path is locked in an incompatible mode, then Tj must be delayed.

Suppose now that transaction Tk wishes to lock the entire database. To do so, it simply must lock the root of the hierarchy. Note, however, that Tk should not succeed in locking the root node, since Ti is currently holding a lock on part of the tree (specifically, on file Fb). But how does the system determine if the root node can be locked? One possibility is for it to search the entire tree. This solution, however, de- feats the whole purpose of the multiple-granularity locking scheme. A more efficient way to gain this knowledge is to introduce a new class of lock modes, called inten- tion lock modes. If a node is locked in an intention mode, explicit locking is being done at a lower level of the tree (that is, at a finer granularity). Intention locks are put on all the ancestors of a node before that node is locked explicitly. Thus, a transaction does not need to search the entire tree to determine whether it can lock a node successfully. A transaction wishing to lock a node—say, Q—must traverse a path in the tree from the root to Q. While traversing the tree, the transaction locks the various nodes in an intention mode.

There is an intention mode associated with shared mode, and there is one with exclusive mode. If a node is locked in intention-shared (IS) mode, explicit locking is being done at a lower level of the tree, but with only shared-mode locks. Similarly, if a node is locked in intention-exclusive (IX) mode, then explicit locking is being done at a lower level, with exclusive-mode or shared-mode locks. Finally, if a node is locked in shared and intention-exclusive (SIX) mode, the subtree rooted by that node is locked explicitly in shared mode, and that explicit locking is being done at a lower level with exclusive-mode locks. The compatibility function for these lock modes is in Figure 16.17.

The multiple-granularity locking protocol, which ensures serializability, is this:

Each transaction Ti can lock a node Q by following these rules:

1. It must observe the lock-compatibility function of Figure 16.17.

2. It must lock the root of the tree first, and can lock it in any mode.

3. It can lock a node Q in S or IS mode only if it currently has the parent of Q locked in either IX or IS mode.

4. It can lock a node Q in X, SIX, or IX mode only if it currently has the parent of Q locked in either IX or SIX mode.

5. It can lock a node only if it has not previously unlocked any node (that is, Ti is two phase).

6. It can unlock a node Q only if it currently has none of the children of Q locked.

Observe that the multiple-granularity protocol requires that locks be acquired in top- down (root-to-leaf) order, whereas locks must be released in bottom-up (leaf-to-root) order.

As an illustration of the protocol, consider the tree of Figure 16.16 and these trans- actions:

• Suppose that transaction T18 reads record ra2 in file Fa. Then, T18 needs to lock the database, area A1, and Fa in IS mode (and in that order), and finally to lock ra2 in S mode.

• Suppose that transaction T19 modifies record ra9 in file Fa. Then, T19 needs to lock the database, area A1, and file Fa in IX mode, and finally to lock ra9 in X mode.

• Suppose that transaction T20 reads all the records in file Fa. Then, T20 needs to lock the database and area A1 (in that order) in IS mode, and finally to lock Fa in S mode.

• Suppose that transaction T21 reads the entire database. It can do so after locking the database in S mode.

We note that transactions T18, T20, and T21 can access the database concurrently. Transaction T19 can execute concurrently with T18, but not with either T20 or T21.

This protocol enhances concurrency and reduces lock overhead. It is particularly useful in applications that include a mix of

• Short transactions that access only a few data items

• Long transactions that produce reports from an entire file or set of files There is a similar locking protocol that is applicable to database systems in which data granularities are organized in the form of a directed acyclic graph. See the bibliographical notes for additional references. Deadlock is possible in the protocol that we have, as it is in the two-phase locking protocol. There are techniques to reduce deadlock frequency in the multiple-granularity protocol, and also to eliminate dead- lock entirely. These techniques are referenced in the bibliographical notes.

Multiversion Schemes

The concurrency-control schemes discussed thus far ensure serializability by either delaying an operation or aborting the transaction that issued the operation. For ex- ample, a read operation may be delayed because the appropriate value has not been written yet; or it may be rejected (that is, the issuing transaction must be aborted) because the value that it was supposed to read has already been overwritten. These difficulties could be avoided if old copies of each data item were kept in a system.

In multiversion concurrency control schemes, each write(Q) operation creates a new version of Q. When a transaction issues a read(Q) operation, the concurrency- control manager selects one of the versions of Q to be read. The concurrency-control

scheme must ensure that the version to be read is selected in a manner that ensures serializability. It is also crucial, for performance reasons, that a transaction be able to determine easily and quickly which version of the data item should be read.

Multiversion Timestamp Ordering

The most common transaction ordering technique used by multiversion schemes is timestamping. With each transaction Ti in the system, we associate a unique static timestamp, denoted by TS(Ti). The database system assigns this timestamp before the transaction starts execution, as described in Section 16.2.

With each data item Q, a sequence of versions <Q1, Q2,.. ., Qm> is associated. Each version Qk contains three data fields:

• Content is the value of version Qk .

• W-timestamp(Qk ) is the timestamp of the transaction that created version Qk .

• R-timestamp(Qk ) is the largest timestamp of any transaction that successfully read version Qk .

A transaction—say, Ti—creates a new version Qk of data item Q by issuing a write(Q) operation. The content field of the version holds the value written by Ti. The system initializes the W-timestamp and R-timestamp to TS(Ti). It updates the R-timestamp value of Qk whenever a transaction Tj reads the content of Qk , and R-timestamp(Qk ) < TS(Tj ).

The multiversion timestamp-ordering scheme presented next ensures serializ- ability. The scheme operates as follows. Suppose that transaction Ti issues a read(Q) or write(Q) operation. Let Qk denote the version of Q whose write timestamp is the largest write timestamp less than or equal to TS(Ti).

1. If transaction Ti issues a read(Q), then the value returned is the content of version Qk .

2. If transaction Ti issues write(Q), and if TS(Ti) < R-timestamp(Qk ), then the sys- tem rolls back transaction Ti. On the other hand, if TS(Ti) = W-timestamp(Qk ), the system overwrites the contents of Qk ; otherwise it creates a new version of Q.

The justification for rule 1 is clear. A transaction reads the most recent version that comes before it in time. The second rule forces a transaction to abort if it is “too late” in doing a write. More precisely, if Ti attempts to write a version that some other transaction would have read, then we cannot allow that write to succeed.

Versions that are no longer needed are removed according to the following rule.

Suppose that there are two versions, Qk and Qj , of a data item, and that both versions have a W-timestamp less than the timestamp of the oldest transaction in the system.

Then, the older of the two versions Qk and Qj will not be used again, and can be deleted.

The multiversion timestamp-ordering scheme has the desirable property that a read request never fails and is never made to wait. In typical database systems, where reading is a more frequent operation than is writing, this advantage may be of major practical significance.

The scheme, however, suffers from two undesirable properties. First, the reading of a data item also requires the updating of the R-timestamp field, resulting in two potential disk accesses, rather than one. Second, the conflicts between transactions are resolved through rollbacks, rather than through waits. This alternative may be expensive. Section 16.5.2 describes an algorithm to alleviate this problem.

This multiversion timestamp-ordering scheme does not ensure recoverability and cascadelessness. It can be extended in the same manner as the basic timestamp- ordering scheme, to make it recoverable and cascadeless.

Multiversion Two-Phase Locking

The multiversion two-phase locking protocol attempts to combine the advantages of multiversion concurrency control with the advantages of two-phase locking. This protocol differentiates between read-only transactions and update transactions.

Update transactions perform rigorous two-phase locking; that is, they hold all locks up to the end of the transaction. Thus, they can be serialized according to their commit order. Each version of a data item has a single timestamp. The timestamp in this case is not a real clock-based timestamp, but rather is a counter, which we will call the ts-counter, that is incremented during commit processing.

Read-only transactions are assigned a timestamp by reading the current value of ts-counter before they start execution; they follow the multiversion timestamp- ordering protocol for performing reads. Thus, when a read-only transaction Ti issues a read(Q), the value returned is the contents of the version whose timestamp is the largest timestamp less than TS(Ti).

When an update transaction reads an item, it gets a shared lock on the item, and reads the latest version of that item. When an update transaction wants to write an item, it first gets an exclusive lock on the item, and then creates a new version of the data item. The write is performed on the new version, and the timestamp of the new version is initially set to a value ∞, a value greater than that of any possible timestamp.

When the update transaction Ti completes its actions, it carries out commit processing: First, Ti sets the timestamp on every version it has created to 1 more than the value of ts-counter; then, Ti increments ts-counter by 1. Only one update transaction is allowed to perform commit processing at a time.

As a result, read-only transactions that start after Ti increments ts-counter will see the values updated by Ti, whereas those that start before Ti increments ts-counter will see the value before the updates by Ti. In either case, read-only transactions never need to wait for locks. Multiversion two-phase locking also ensures that schedules are recoverable and cascadeless.

Versions are deleted in a manner like that of multiversion timestamp ordering.

Suppose there are two versions, Qk and Qj , of a data item, and that both versions have a timestamp less than the timestamp of the oldest read-only transaction in the system. Then, the older of the two versions Qk and Qj will not be used again and can be deleted.

Multiversion two-phase locking or variations of it are used in some commercial database systems.