Distributed Databases:Availability
Availability
One of the goals in using distributed databases is high availability; that is, the data- base must function almost all the time. In particular, since failures are more likely in large distributed systems, a distributed database must continue functioning even when there are various types of failures. The ability to continue functioning even during failures is referred to as robustness.
For a distributed system to be robust, it must detect failures, reconfigure the system so that computation may continue, and recover when a processor or a link is repaired.
The different types of failures are handled in different ways. For example, message loss is handled by retransmission. Repeated retransmission of a message across a link, without receipt of an acknowledgment, is usually a symptom of a link failure. The network usually attempts to find an alternative route for the message. Failure to find such a route is usually a symptom of network partition.
It is generally not possible, however, to differentiate clearly between site failure and network partition. The system can usually detect that a failure has occurred, but it may not be able to identify the type of failure. For example, suppose that site S1 is not able to communicate with S2. It could be that S2 has failed. However, another possibility is that the link between S1 and S2 has failed, resulting in network partition. The problem is partly addressed by using multiple links between sites, so that even if one link fails the sites will remain connected. However, multiple link failure can still occur, so there are situations where we cannot be sure whether a site failure or network partition has occurred.
Suppose that site S1 has discovered that a failure has occurred. It must then initiate a procedure that will allow the system to reconfigure, and to continue with the normal mode of operation.
• If transactions were active at a failed/inaccessible site at the time of the failure, these transactions should be aborted. It is desirable to abort such transactions promptly, since they may hold locks on data at sites that are still active; waiting for the failed/inaccessible site to become accessible again may impede other transactions at sites that are operational.
However, in some cases, when data objects are replicated it may be possible to proceed with reads and updates even though some replicas are inaccessible. In this case, when a failed site recovers, if it had replicas of any data object, it must obtain the current values of these data objects, and must ensure that it receives all future updates. We address this issue in Section 19.6.1.
• If replicated data are stored at a failed/inaccessible site, the catalog should be updated so that queries do not reference the copy at the failed site. When a site rejoins, care must be taken to ensure that data at the site is consistent, as we will see in Section 19.6.3.
• If a failed site is a central server for some subsystem, an election must be held to determine the new server (see Section 19.6.5). Examples of central servers include a name server, a concurrency coordinator, or a global deadlock detector.
Since it is, in general, not possible to distinguish between network link failures and site failures, any reconfiguration scheme must be designed to work correctly in case of a partitioning of the network. In particular, these situations must be avoided:
• Two or more central servers are elected in distinct partitions.
• More than one partition updates a replicated data item.
Majority-Based Approach
The majority-based approach to distributed concurrency control in Section 19.5.1.4 can be modified to work in spite of failures. In this approach, each data object stores with it a version number to detect when it was last written to. Whenever a transaction writes an object it also updates the version number in this way:
• If data object a is replicated in n different sites, then a lock-request message must be sent to more than one-half of the n sites in which a is stored. The transaction does not operate on a until it has successfully obtained a lock on a majority of the replicas of a.
• Read operations look at all replicas on which a lock has been obtained, and read the value from the replica that has the highest version number. (Option- ally, they may also write this value back to replicas with lower version numbers.) Writes read all the replicas just like reads to find the highest version number (this step would normally have been performed earlier in the trans- action by a read, and the result can be reused). The new version number is one more than the highest version number. The write operation writes all the replicas on which it has obtained locks, and sets the version number at all the replicas to the new version number.
Failures during a transaction (whether network partitions or site failures) can be tolerated as long as (1) the sites available at commit contain a majority of replicas of all the objects written to and (2) during reads, a majority of replicas are read to find the version numbers. If these requirements are violated, the transaction must be aborted. As long as the requirements are satisfied, the two-phase commit protocol can be used, as usual, on the sites that are available.
In this scheme, reintegration is trivial; nothing needs to be done. This is because writes would have updated a majority of the replicas, while reads will read a majority of the replicas and find at least one replica that has the latest version.
The version numbering technique used with the majority protocol can also be used to make the quorum consensus protocol work in the presence of failures. We leave the (straightforward) details to the reader. However, the danger of failures preventing the system from processing transactions increases if some sites are given higher weights.
Read One, Write All Available Approach
As a special case of quorum consensus, we can employ the biased protocol by giving unit weights to all sites, setting the read quorum to 1, and setting the write quorum to n (all sites). In this special case, there is no need to use version numbers; however, if even a single site containing a data item fails, no write to the item can proceed, since the write quorum will not be available. This protocol is called the read one, write all protocol since all replicas must be written.
To allow work to proceed in the event of failures, we would like to be able to use a read one, write all available protocol. In this approach, a read operation proceeds as in the read one, write all scheme; any available replica can be read, and a read lock is obtained at that replica. A write operation is shipped to all replicas; and write locks are acquired on all the replicas. If a site is down, the transaction manager proceeds without waiting for the site to recover.
While this approach appears very attractive, there are several complications. In particular, temporary communication failure may cause a site to appear to be un- available, resulting in a write not being performed, but when the link is restored, the site is not aware that it has to perform some reintegration actions to catch up on writes it has lost. Further, if the network partitions, each partition may proceed to update the same data item, believing that sites in the other partitions are all dead.
The read one, write all available scheme can be used if there is never any network partitioning, but it can result in inconsistencies in the event of network partitions.
Site Reintegration
Reintegration of a repaired site or link into the system requires care. When a failed site recovers, it must initiate a procedure to update its system tables to reflect changes made while it was down. If the site had replicas of any data items, it must obtain the current values of these data items and ensure that it receives all future updates. Reintegration of a site is more complicated than it may seem to be at first glance, since there may be updates to the data items processed during the time that the site is recovering.
An easy solution is to halt the entire system temporarily while the failed site rejoins it. In most applications, however, such a temporary halt is unacceptably disruptive. Techniques have been developed to allow failed sites to reintegrate while concurrent updates to data items proceed concurrently. Before a read or write lock is granted on any data item, the site must ensure that it has caught up on all updates to the data item. If a failed link recovers, two or more partitions can be rejoined. Since a partitioning of the network limits the allowable operations by some or all sites, all sites should be informed promptly of the recovery of the link. See the bibliographical notes for more information on recovery in distributed systems.
Comparison with Remote Backup
Remote backup systems, which we studied in Section 17.10, and replication in distributed databases are two alternative approaches to providing high availability. The main difference between the two schemes is that with remote backup systems, actions such as concurrency control and recovery are performed at a single site, and only data and log records are replicated at the other site. In particular, remote backup systems help avoid two-phase commit, and its resultant overheads. Also, transactions need to contact only one site (the primary site), and thus avoid the overhead of running transaction code at multiple sites. Thus remote backup systems offer a lower-cost approach to high availability than replication.
On the other hand, replication can provide greater availability by having multiple replicas available, and using the majority protocol.
Coordinator Selection
Several of the algorithms that we have presented require the use of a coordinator. If the coordinator fails because of a failure of the site at which it resides, the system can continue execution only by restarting a new coordinator on another site. One way to continue execution is by maintaining a backup to the coordinator, which is ready to assume responsibility if the coordinator fails.
A backup coordinator is a site that, in addition to other tasks, maintains enough information locally to allow it to assume the role of coordinator with minimal disruption to the distributed system. All messages directed to the coordinator are received
by both the coordinator and its backup. The backup coordinator executes the same algorithms and maintains the same internal state information (such as, for a concurrency coordinator, the lock table) as does the actual coordinator. The only difference in function between the coordinator and its backup is that the backup does not take any action that affects other sites. Such actions are left to the actual coordinator.
In the event that the backup coordinator detects the failure of the actual coordinator, it assumes the role of coordinator. Since the backup has all the information available to it that the failed coordinator had, processing can continue without interruption.
The prime advantage to the backup approach is the ability to continue processing immediately. If a backup were not ready to assume the coordinator’s responsibility, a newly appointed coordinator would have to seek information from all sites in the system so that it could execute the coordination tasks. Frequently, the only source of some of the requisite information is the failed coordinator. In this case, it may be necessary to abort several (or all) active transactions, and to restart them under the control of the new coordinator.
Thus, the backup-coordinator approach avoids a substantial amount of delay while the distributed system recovers from a coordinator failure. The disadvantage is the overhead of duplicate execution of the coordinator’s tasks. Furthermore, a coordinator and its backup need to communicate regularly to ensure that their activities are synchronized.
In short, the backup-coordinator approach incurs overhead during normal processing to allow fast recovery from a coordinator failure.
In the absence of a designated backup coordinator, or in order to handle multiple failures, a new coordinator may be chosen dynamically by sites that are live. Election algorithms enable the sites to choose the site for the new coordinator in a decentralized manner. Election algorithms require that a unique identification number be associated with each active site in the system.
The bully algorithm for election works as follows. To keep the notation and the discussion simple, assume that the identification number of site Si is i and that the chosen coordinator will always be the active site with the largest identification number. Hence, when a coordinator fails, the algorithm must elect the active site that has the largest identification number. The algorithm must send this number to each active site in the system. In addition, the algorithm must provide a mechanism by which a site recovering from a crash can identify the current coordinator. Suppose that site Si sends a request that is not answered by the coordinator within a prespecified time interval T. In this situation, it is assumed that the coordinator has failed, and Si tries to elect itself as the site for the new coordinator.
Site Si sends an election message to every site that has a higher identification number. Site Si then waits, for a time interval T, for an answer from any one of these sites. If it receives no response within time T, it assumes that all sites with numbers greater than i have failed, and it elects itself as the site for the new coordinator and sends a message to inform all active sites with identification numbers lower than i that it is the site at which the new coordinator resides.
If Si does receive an answer, it begins a time interval T l, to receive a message informing it that a site with a higher identification number has been elected. (Some
other site is electing itself coordinator, and should report the results within time T l.) If Si receives no message within T l, then it assumes the site with a higher number has failed, and site Si restarts the algorithm.
After a failed site recovers, it immediately begins execution of the same algorithm.
If there are no active sites with higher numbers, the recovered site forces all sites with lower numbers to let it become the coordinator site, even if there is a currently active coordinator with a lower number. It is for this reason that the algorithm is termed the bully algorithm.
Distributed Query Processing
In Chapter 14, we saw that there are a variety of methods for computing the answer to a query. We examined several techniques for choosing a strategy for processing a query that minimize the amount of time that it takes to compute the answer. For cen- tralized systems, the primary criterion for measuring the cost of a particular strategy is the number of disk accesses. In a distributed system, we must take into account several other matters, including
• The cost of data transmission over the network
• The potential gain in performance from having several sites process parts of the query in parallel The relative cost of data transfer over the network and data transfer to and from disk varies widely depending on the type of network and on the speed of the disks. Thus, in general, we cannot focus solely on disk costs or on network costs. Rather, we must find a good tradeoff between the two.
Query Transformation
Consider an extremely simple query: “Find all the tuples in the account relation.” Al- though the query is simple — indeed, trivial—processing it is not trivial, since the account relation may be fragmented, replicated, or both, as we saw in Section 19.2. If the account relation is replicated, we have a choice of replica to make. If no replicas are fragmented, we choose the replica for which the transmission cost is lowest. However, if a replica is fragmented, the choice is not so easy to make, since we need to compute several joins or unions to reconstruct the account relation. In this case, the number of strategies for our simple example may be large. Query optimization by exhaustive enumeration of all alternative strategies may not be practical in such situations.
Fragmentation transparency implies that a user may write a query such as
This expression is the empty set, regardless of the contents of the account relation.
Thus, our final strategy is for the Hillside site to return account1 as the result of the query.
Simple Join Processing
As we saw in Chapter 13, a major decision in the selection of a query-processing strategy is choosing a join strategy. Consider the following relational-algebra expression:
Assume that the three relations are neither replicated nor fragmented, and that ac- count is stored at site S1, depositor at S2, and branch at S3. Let SI denote the site at which the query was issued. The system needs to produce the result at site SI . Among the possible strategies for processing this query are these:
• Ship copies of all three relations to site SI . Using the techniques of Chapter 13, choose a strategy for processing the entire query locally at site SI .
• Ship a copy of the account relation to site S2, and compute temp1 = account depositor at S2. Ship temp1 from S2 to S3, and compute temp2 = temp1 branch at S3. Ship the result temp2 to SI .
• Devise strategies similar to the previous one, with the roles of S1, S2, S3 ex- changed.
No one strategy is always the best one. Among the factors that must be considered are the volume of data being shipped, the cost of transmitting a block of data be- tween a pair of sites, and the relative speed of processing at each site. Consider the first two strategies listed. If we ship all three relations to SI , and indices exist on these relations, we may need to re-create these indices at SI . This re-creation of in- dices entails extra processing overhead and extra disk accesses. However, the second strategy has the disadvantage that a potentially large relation (customer account)
must be shipped from S2 to S3. This relation repeats the address data for a customer once for each account that the customer has. Thus, the second strategy may result in extra network transmission compared to the first strategy.
Semijoin Strategy
Suppose that we wish to evaluate the expression r1 r2, where r1 and r2 are stored at sites S1 and S2, respectively. Let the schemas of r1 and r2 be R1 and R2. Suppose that we wish to obtain the result at S1. If there are many tuples of r2 that do not join with any tuple of r1, then shipping r2 to S1 entails shipping tuples that fail to contribute to the result. We want to remove such tuples before shipping data to S1, particularly if network costs are high.
A possible strategy to accomplish all this is:
This strategy is particularly advantageous when relatively few tuples of r2 con- tribute to the join. This situation is likely to occur if r1 is the result of a relational- algebra expression involving selection. In such a case, temp2 may have significantly fewer tuples than r2. The cost savings of the strategy result from having to ship only temp2, rather than all of r2, to S1. Additional cost is incurred in shipping temp1 to S2. If a sufficiently small fraction of tuples in r2 contribute to the join, the overhead of shipping temp1 will be dominated by the savings of shipping only a fraction of the tuples in r2.
This strategy is called a semijoin strategy, after the semijoin operator of the rela
For joins of several relations, this strategy can be extended to a series of semijoin steps. A substantial body of theory has been developed regarding the use of semijoins for query optimization. Some of this theory is referenced in the bibliographical notes.


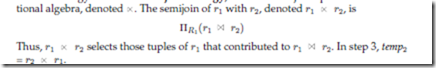



Comments
Post a Comment