Transactions:Serializability

Serializability

The database system must control concurrent execution of transactions, to ensure that the database state remains consistent. Before we examine how the database

system can carry out this task, we must first understand which schedules will en- sure consistency, and which schedules will not.

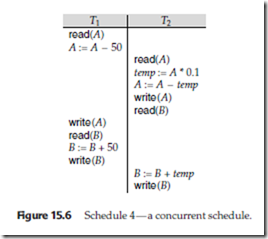
Since transactions are programs, it is computationally difficult to determine exactly what operations a transaction performs and how operations of various trans- actions interact. For this reason, we shall not interpret the type of operations that a transaction can perform on a data item. Instead, we consider only two operations: read and write. We thus assume that, between a read(Q) instruction and a write(Q) instruction on a data item Q, a transaction may perform an arbitrary sequence of operations on the copy of Q that is residing in the local buffer of the transaction. Thus, the only significant operations of a transaction, from a scheduling point of view, are its read and write instructions. We shall therefore usually show only read and write instructions in schedules, as we do in schedule 3 in Figure 15.7.

In this section, we discuss different forms of schedule equivalence; they lead to the notions of conflict serializability and view serializability.

Conflict Serializability

Let us consider a schedule S in which there are two consecutive instructions Ii and Ij , of transactions Ti and Tj , respectively (i j= j). If Ii and Ij refer to different data items, then we can swap Ii and Ij without affecting the results of any instruction in the schedule. However, if Ii and Ij refer to the same data item Q, then the order of the two steps may matter. Since we are dealing with only read and write instructions,

there are four cases that we need to consider:

Thus, only in the case where both Ii and Ij are read instructions does the relative order of their execution not matter.

We say that Ii and Ij conflict if they are operations by different transactions on the same data item, and at least one of these instructions is a write operation.

To illustrate the concept of conflicting instructions, we consider schedule 3, in Figure 15.7. The write(A) instruction of T1 conflicts with the read(A) instruction of T2. However, the write(A) instruction of T2 does not conflict with the read(B) instruction of T1, because the two instructions access different data items.

Let Ii and Ij be consecutive instructions of a schedule S. If Ii and Ij are instructions of different transactions and Ii and Ij do not conflict, then we can swap the order of Ii and Ij to produce a new schedule S1. We expect S to be equivalent to S1, since all instructions appear in the same order in both schedules except for Ii and Ij , whose order does not matter.

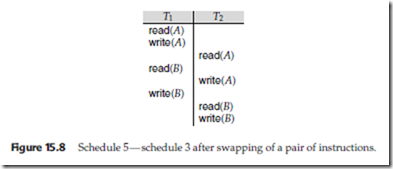
Since the write(A) instruction of T2 in schedule 3 of Figure 15.7 does not conflict with the read(B) instruction of T1, we can swap these instructions to generate an equivalent schedule, schedule 5, in Figure 15.8. Regardless of the initial system state, schedules 3 and 5 both produce the same final system state.

We continue to swap nonconflicting instructions:

• Swap the read(B) instruction of T1 with the read(A) instruction of T2.

• Swap the write(B) instruction of T1 with the write(A) instruction of T2.

• Swap the write(B) instruction of T1 with the read(A) instruction of T2.

The final result of these swaps, schedule 6 of Figure 15.9, is a serial schedule. Thus, we have shown that schedule 3 is equivalent to a serial schedule. This equivalence implies that, regardless of the initial system state, schedule 3 will produce the same final state as will some serial schedule.

If a schedule S can be transformed into a schedule S1 by a series of swaps of non- conflicting instructions, we say that S and S1 are conflict equivalent.

In our previous examples, schedule 1 is not conflict equivalent to schedule 2. How- ever, schedule 1 is conflict equivalent to schedule 3, because the read(B) and write(B) instruction of T1 can be swapped with the read(A) and write(A) instruction of T2.

The concept of conflict equivalence leads to the concept of conflict serializability.

We say that a schedule S is conflict serializable if it is conflict equivalent to a serial schedule. Thus, schedule 3 is conflict serializable, since it is conflict equivalent to the serial schedule 1.

Finally, consider schedule 7 of Figure 15.10; it consists of only the significant operations (that is, the read and write) of transactions T3 and T4. This schedule is not conflict serializable, since it is not equivalent to either the serial schedule <T3,T4> or the serial schedule <T4,T3>.

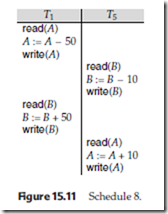
It is possible to have two schedules that produce the same outcome, but that are not conflict equivalent. For example, consider transaction T5, which transfers $10

from account B to account A. Let schedule 8 be as defined in Figure 15.11. We claim that schedule 8 is not conflict equivalent to the serial schedule <T1,T5>, since, in schedule 8, the write(B) instruction of T5 conflicts with the read(B) instruction of T1. Thus, we cannot move all the instructions of T1 before those of T5 by swapping con- secutive nonconflicting instructions. However, the final values of accounts A and B after the execution of either schedule 8 or the serial schedule <T1,T5> are the same — $960 and $2040, respectively.

We can see from this example that there are less stringent definitions of schedule equivalence than conflict equivalence. For the system to determine that schedule 8 produces the same outcome as the serial schedule <T1,T5>, it must analyze the computation performed by T1 and T5, rather than just the read and write operations. In general, such analysis is hard to implement and is computationally expensive. How ever, there are other definitions of schedule equivalence based purely on the read and write operations. We will consider one such definition in the next section.

View Serializability

In this section, we consider a form of equivalence that is less stringent than conflict equivalence, but that, like conflict equivalence, is based on only the read and write operations of transactions.

Consider two schedules S and S1, where the same set of transactions participates in both schedules. The schedules S and S1 are said to be view equivalent if three conditions are met:

1. For each data item Q, if transaction Ti reads the initial value of Q in schedule S, then transaction Ti must, in schedule S1, also read the initial value of Q.

2. For each data item Q, if transaction Ti executes read(Q) in schedule S, and if that value was produced by a write(Q) operation executed by transaction Tj , then the read(Q) operation of transaction Ti must, in schedule S1, also read the value of Q that was produced by the same write(Q) operation of transaction Tj .

3. For each data item Q, the transaction (if any) that performs the final write(Q) operation in schedule S must perform the final write(Q) operation in schedule S1.

Conditions 1 and 2 ensure that each transaction reads the same values in both schedules and, therefore, performs the same computation. Condition 3, coupled with conditions 1 and 2, ensures that both schedules result in the same final system state.

In our previous examples, schedule 1 is not view equivalent to schedule 2, since, in schedule 1, the value of account A read by transaction T2 was produced by T1, whereas this case does not hold in schedule 2. However, schedule 1 is view equivalent to schedule 3, because the values of account A and B read by transaction T2 were produced by T1 in both schedules.

The concept of view equivalence leads to the concept of view serializability. We say that a schedule S is view serializable if it is view equivalent to a serial schedule.

As an illustration, suppose that we augment schedule 7 with transaction T6, and obtain schedule 9 in Figure 15.12. Schedule 9 is view serializable. Indeed, it is view equivalent to the serial schedule <T3, T4, T6>, since the one read(Q) instruction reads the initial value of Q in both schedules, and T6 performs the final write of Q in both schedules.

Every conflict-serializable schedule is also view serializable, but there are view serializable schedules that are not conflict serializable. Indeed, schedule 9 is not conflict serializable, since every pair of consecutive instructions conflicts, and, thus, no swapping of instructions is possible.

Observe that, in schedule 9, transactions T4 and T6 perform write(Q) operations without having performed a read(Q) operation. Writes of this sort are called blind writes. Blind writes appear in any view-serializable schedule that is not conflict serializable.