Extended Relational-Algebra Operations.

Extended Relational-Algebra Operations

The basic relational-algebra operations have been extended in several ways. A simple extension is to allow arithmetic operations as part of projection. An important extension is to allow aggregate operations such as computing the sum of the elements of a

set, or their average. Another important extension is the outer-join operation, which allows relational-algebra expressions to deal with null values, which model missing information.

Generalized Projection

The generalized-projection operation extends the projection operation by allowing arithmetic functions to be used in the projection list. The generalized projection operation has the form

where E is any relational-algebra expression, and each of F1, F2,... , Fn is an arithmetic expression involving constants and attributes in the schema of E. As a special case, the arithmetic expression may be simply an attribute or a constant.

For example, suppose we have a relation credit-info, as in Figure 3.25, which lists the credit limit and expenses so far (the credit-balance on the account). If we want to find how much more each person can spend, we can write the following expression:

The attribute resulting from the expression limit − credit -balance does not have a name. We can apply the rename operation to the result of generalized projection in order to give it a name. As a notational convenience, renaming of attributes can be combined with generalized projection as illustrated below:

The second attribute of this generalized projection has been given the name credit- available. Figure 3.26 shows the result of applying this expression to the relation in Figure 3.25.

Aggregate Functions

Aggregate functions take a collection of values and return a single value as a result. For example, the aggregate function sum takes a collection of values and returns the sum of the values. Thus, the function sum applied on the collection

{1, 1, 3, 4, 4, 11}

returns the value 24. The aggregate function avg returns the average of the values. When applied to the preceding collection, it returns the value 4. The aggregate func- tion count returns the number of the elements in the collection, and returns 6 on the preceding collection. Other common aggregate functions include min and max, which return the minimum and maximum values in a collection; they return 1 and 11, respectively, on the preceding collection.

The collections on which aggregate functions operate can have multiple occurrences of a value; the order in which the values appear is not relevant. Such collections are called multisets. Sets are a special case of multisets where there is only one copy of each element.

To illustrate the concept of aggregation, we shall use the pt-works relation in Figure 3.27, for part-time employees. Suppose that we want to find out the total sum of salaries of all the part-time employees in the bank. The relational-algebra expression for this query is:

The symbol G is the letter G in calligraphic font; read it as “calligraphic G.” The relational-algebra operation G signifies that aggregation is to be applied, and its subscript specifies the aggregate operation to be applied. The result of the expression above is a relation with a single attribute, containing a single row with a numerical value corresponding to the sum of all the salaries of all employees working part-time in the bank.

There are cases where we must eliminate multiple occurrences of a value before computing an aggregate function. If we do want to eliminate duplicates, we use the same function names as before, with the addition of the hyphenated string “distinct” appended to the end of the function name (for example, count-distinct). An example arises in the query “Find the number of branches appearing in the pt-works relation.” In this case, a branch name counts only once, regardless of the number of employees working that branch. We write this query as follows:

For the relation in Figure 3.27, the result of this query is a single row containing the value 3.

Suppose we want to find the total salary sum of all part-time employees at each branch of the bank separately, rather than the sum for the entire bank. To do so, we need to partition the relation pt-works into groups based on the branch, and to apply the aggregate function on each group.

The following expression using the aggregation operator G achieves the desired result:

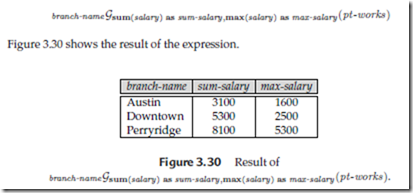
In the expression, the attribute branch-name in the left-hand subscript of G indicates that the input relation pt-works must be divided into groups based on the value of branch-name. Figure 3.28 shows the resulting groups. The expression sum(salary) in the right-hand subscript of G indicates that for each group of tuples (that is, each branch), the aggregation function sum must be applied on the collection of values of the salary attribute. The output relation consists of tuples with the branch name, and the sum of the salaries for the branch, as shown in Figure 3.29.

The general form of the aggregation operation G is as follows:

where E is any relational-algebra expression; G1, G2,... , Gn constitute a list of at- tributes on which to group; each Fi is an aggregate function; and each Ai is an at-

tribute name. The meaning of the operation is as follows. The tuples in the result of expression E are partitioned into groups in such a way that

1. All tuples in a group have the same values for G1, G2,... , Gn.

2. Tuples in different groups have different values for G1, G2,... , Gn.

Thus, the groups can be identified by the values of attributes G1, G2,..., Gn. For each group (g1, g2,... , gn), the result has a tuple (g1, g2,... , gn, a1, a2,... , am) where, for each i, ai is the result of applying the aggregate function Fi on the multiset of values for attribute Ai in the group.

As a special case of the aggregate operation, the list of attributes G1, G2,... , Gn can be empty, in which case there is a single group containing all tuples in the relation. This corresponds to aggregation without grouping.

Going back to our earlier example, if we want to find the maximum salary for part-time employees at each branch, in addition to the sum of the salaries, we write the expression

As in generalized projection, the result of an aggregation operation does not have a name. We can apply a rename operation to the result in order to give it a name. As a notational convenience, attributes of an aggregation operation can be renamed as illustrated below:

Outer Join

The outer-join operation is an extension of the join operation to deal with missing information. Suppose that we have the relations with the following schemas, which contain data on full-time employees:

Consider the employee and ft-works relations in Figure 3.31. Suppose that we want to generate a single relation with all the information (street, city, branch name, and salary) about full-time employees. A possible approach would be to use the natural- join operation as follows:

The result of this expression appears in Figure 3.32. Notice that we have lost the street and city information about Smith, since the tuple describing Smith is absent from the ft-works relation; similarly, we have lost the branch name and salary information about Gates, since the tuple describing Gates is absent from the employee relation.

We can use the outer-join operation to avoid this loss of information. There are actually three forms of the operation: left outer join, denoted  ; right outer join, de- noted ; and full outer join, denoted . All three forms of outer join compute the join, and add extra tuples to the result of the join. The results of the expressions

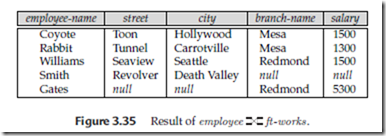
employee ft -works,, employee ft -works, and employee ft -works appear in Figures 3.33, 3.34, and 3.35, respectively.

The left outer join ( ) takes all tuples in the left relation that did not match with any tuple in the right relation, pads the tuples with null values for all other attributes from the right relation, and adds them to the result of the natural join. In Figure 3.33, tuple (Smith, Revolver, Death Valley, null, null) is such a tuple. All information from the left relation is present in the result of the left outer join.

The right outer join ( ) is symmetric with the left outer join: It pads tuples from the right relation that did not match any from the left relation with nulls and adds them to the result of the natural join. In Figure 3.34, tuple (Gates, null, null, Redmond, 5300) is such a tuple. Thus, all information from the right relation is present in the result of the right outer join.

The full outer join( ) does both of those operations, padding tuples from the left relation that did not match any from the right relation, as well as tuples from the right relation that did not match any from the left relation, and adding them to the result of the join. Figure 3.35 shows the result of a full outer join.

Since outer join operations may generate results containing null values, we need to specify how the different relational-algebra operations deal with null values. Section 3.3.4 deals with this issue.

It is interesting to note that the outer join operations can be expressed by the basic relational-algebra operations. For instance, the left outer join operation, r s, can be written as

Null Values∗∗

In this section, we define how the various relational algebra operations deal with null values and complications that arise when a null value participates in an arithmetic operation or in a comparison. As we shall see, there is often more than one possible way of dealing with null values, and as a result our definitions can sometimes be arbitrary. Operations and comparisons on null values should therefore be avoided, where possible.

Since the special value null indicates “value unknown or nonexistent,” any arithmetic operations (such as +, −, ∗, /) involving null values must return a null result.

Similarly, any comparisons (such as <, <=, >, >=, /=) involving a null value evaluate to special value unknown; we cannot say for sure whether the result of the comparison is true or false, so we say that the result is the new truth value unknown.

Comparisons involving nulls may occur inside Boolean expressions involving the and, or, and not operations. We must therefore define how the three Boolean operations deal with the truth value unknown.

• and: (true and unknown) = unknown; (false and unknown) = false; (unknown and unknown) = unknown.

• or: (true or unknown) = true; (false or unknown) = unknown; (unknown or un- known) = unknown.

• not: (not unknown) = unknown.

We are now in a position to outline how the different relational operations deal with null values. Our definitions follow those used in the SQL language.

• select: The selection operation evaluates predicate P in σP (E) on each tuple t in E. If the predicate returns the value true, t is added to the result. Otherwise, if the predicate returns unknown or false, t is not added to the result.

• join: Joins can be expressed as a cross product followed by a selection. Thus, the definition of how selection handles nulls also defines how join operations handle nulls.

In a natural join, say r s, we can see from the above definition that if two tuples, tr ∈ r and ts ∈ s, both have a null value in a common attribute, then the tuples do not match.

• projection: The projection operation treats nulls just like any other value when eliminating duplicates. Thus, if two tuples in the projection result are exactly the same, and both have nulls in the same fields, they are treated as duplicates.

The decision is a little arbitrary since, without knowing the actual value, we do not know if the two instances of null are duplicates or not.

• union, intersection, difference: These operations treat nulls just as the projection operation does; they treat tuples that have the same values on all fields as duplicates even if some of the fields have null values in both tuples.

The behavior is rather arbitrary, especially in the case of intersection and difference, since we do not know if the actual values (if any) represented by the nulls are the same.

• generalized projection: We outlined how nulls are handled in expressions at the beginning of Section 3.3.4. Duplicate tuples containing null values are handled as in the projection operation.

• aggregate: When nulls occur in grouping attributes, the aggregate operation treats them just as in projection: If two tuples are the same on all grouping attributes, the operation places them in the same group, even if some of their attribute values are null.

When nulls occur in aggregated attributes, the operation deletes null values at the outset, before applying aggregation. If the resultant multiset is empty, the aggregate result is null.

Note that the treatment of nulls here is different from that in ordinary arithmetic expressions; we could have defined the result of an aggregate operation as null if even one of the aggregated values is null. However, this would mean a single unknown value in a large group could make the aggregate result on the group to be null, and we would lose a lot of useful information.

• outer join: Outer join operations behave just like join operations, except on tuples that do not occur in the join result. Such tuples may be added to the result (depending on whether the operation is , , or ), padded with nulls.